bezier_tangent()

bezier_tangent()#

Calculates the tangent of a point on a Bezier curve.

Examples#

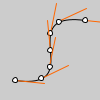
example picture for bezier_tangent()

def setup():
    py5.no_fill()
    py5.bezier(85, 20, 10, 10, 90, 90, 15, 80)
    steps = 6
    py5.fill(255)
    for i in range(0, steps+1):
        t = i / steps
        # get the location of the point
        x = py5.bezier_point(85, 10, 90, 15, t)
        y = py5.bezier_point(20, 10, 90, 80, t)
        # get the tangent points
        tx = py5.bezier_tangent(85, 10, 90, 15, t)
        ty = py5.bezier_tangent(20, 10, 90, 80, t)
        # calculate an angle from_ the tangent points
        a = py5.atan2(ty, tx)
        a += py5.PI
        py5.stroke(255, 102, 0)
        py5.line(x, y, py5.cos(a)*30+x, py5.sin(a)*30+y)
        # the following line of code makes a line
        # inverse of the above line
        #line(x, y, cos(a)*-30+x, sin(a)*-30+y)
        py5.stroke(0)
        py5.ellipse(x, y, 5, 5)

example picture for bezier_tangent()

def setup():
    py5.no_fill()
    py5.bezier(85, 20, 10, 10, 90, 90, 15, 80)
    py5.stroke(255, 102, 0)
    steps = 16
    for i in range(0, steps+1):
        t = i / steps
        x = py5.bezier_point(85, 10, 90, 15, t)
        y = py5.bezier_point(20, 10, 90, 80, t)
        tx = py5.bezier_tangent(85, 10, 90, 15, t)
        ty = py5.bezier_tangent(20, 10, 90, 80, t)
        a = py5.atan2(ty, tx)
        a -= py5.HALF_PI
        py5.line(x, y, py5.cos(a)*8+x, py5.sin(a)*8+y)

Description#

Calculates the tangent of a point on a Bezier curve. There is a good definition of tangent on Wikipedia.

Underlying Processing method: bezierTangent

Signatures#

bezier_tangent(
    a: float,  # coordinate of first point on the curve
    b: float,  # coordinate of first control point
    c: float,  # coordinate of second control point
    d: float,  # coordinate of second point on the curve
    t: float,  # value between 0 and 1
    /,
) -> float

Updated on March 06, 2023 02:49:26am UTC

Contents